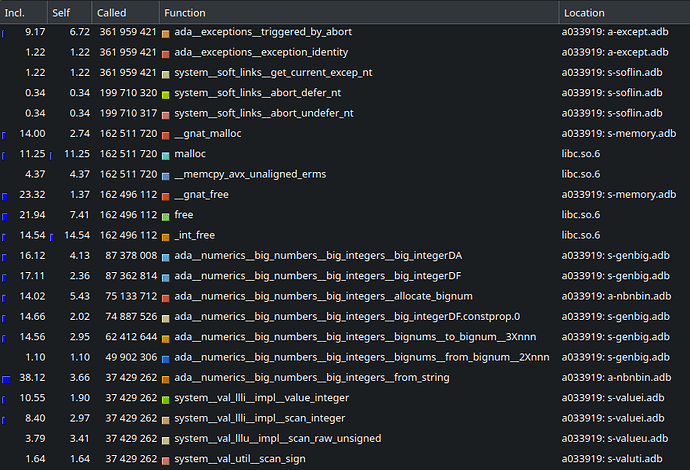
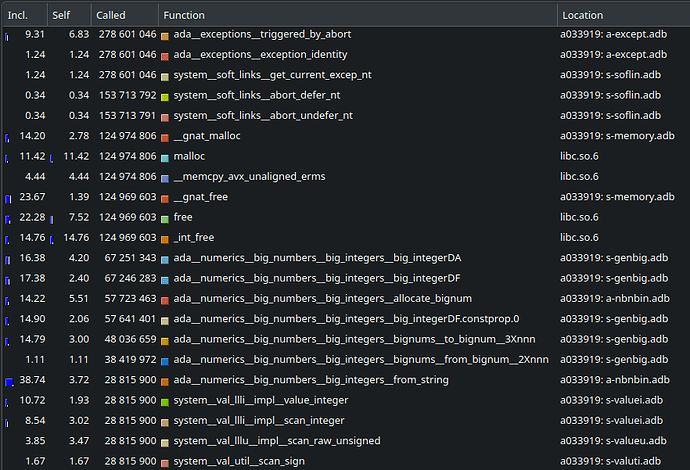
Hi;
Bug(s) in my Ada program for Number Sequence (OEIS:A033919 - Odd k for which k+2^m is composite for all m < k) Rosetta Code
Here’s my code. Please show me where I screwed up!
-- Has bug(s)!
-- Rosetta Code Task written in Ada
-- Smallest number k such that k+2^m is composite for all m less than k
-- https://rosettacode.org/wiki/Smallest_number_k_such_that_k%2B2%5Em_is_composite_for_all_m_less_than_k
-- loosely translated from the Python solution
-- November 2024, R. B. E.
pragma Ada_2022;
with Ada.Text_IO; -- use Ada.Text_IO;
with Ada.Integer_Text_IO; -- use Ada.Integer_Text_IO;
with Ada.Numerics.Big_Numbers.Big_Integers; use Ada.Numerics.Big_Numbers.Big_Integers;
procedure Smallest_Number_K is
function Is_Prime (N : in Big_Integer) return Boolean is
Big_0 : Big_Natural := To_Big_Integer (0);
Big_2 : Big_Natural := To_Big_Integer (2);
Big_3 : Big_Natural := To_Big_Integer (3);
Big_Temp : Big_Natural := To_Big_Integer (5);
begin
if N < Big_2 then
return False;
end if;
if N mod Big_2 = Big_0 then
return N = Big_2;
end if;
if N mod Big_3 = Big_0 then
return N = Big_3;
end if;
while Big_Temp * Big_Temp <= N loop
if N mod Big_Temp = Big_0 then
return False;
end if;
Big_Temp := Big_Temp + Big_2;
if N mod Big_Temp = Big_0 then
return False;
end if;
Big_Temp := Big_Temp + 4;
end loop;
return True;
end Is_Prime;
type Powers_of_Two_Table is array (0..5200) of Big_Positive; -- 5200 is just a rough upper limit guess of how many I need
Powers_of_Two : Powers_of_Two_Table;
procedure Load_Powers_of_Two (Powers_of_Two : in out Powers_of_Two_Table) is
begin
for I in Powers_of_Two'Range loop
if I = 0 then
Powers_of_Two (I) := To_Big_Integer (1);
elsif I = 1 then
Powers_of_Two (I) := To_Big_Integer (2);
else
Powers_of_Two (I) := Powers_of_Two (I-1) * To_Big_Integer (2);
end if;
end loop;
end Load_Powers_of_Two;
procedure Show_Powers_of_Two (Powers_of_Two : in Powers_of_Two_Table) is
begin
for I in Powers_of_Two'Range loop
Ada.Text_IO.Put_Line (To_String (Powers_of_Two (I)));
end loop;
end Show_Powers_of_Two;
function Is_A033919 (Powers_of_Two : in Powers_of_Two_Table; K : in Positive) return Boolean is
N : Big_Positive;
begin
if K = 1 then
return False;
else
for M in 1..K loop
N := Powers_of_Two (M) + To_Big_Integer (K);
Ada.Text_IO.Put ("DEBUG: (function Is_A033919) : N is ");
Ada.Text_IO.Put_Line (To_String (N));
if Is_Prime (N) then
return False;
end if;
end loop;
return True;
end if;
end Is_A033919;
Sequence_Number : Natural := 0;
Max_Sequence_Number : Positive := 5;
I : Positive := 1;
begin
Load_Powers_of_Two (Powers_of_Two);
-- Show_Powers_of_Two (Powers_of_Two);
loop
Ada.Text_IO.Put ("DEBUG: (main program): I is ");
Ada.Integer_Text_IO.Put (I, 0);
Ada.Text_IO.New_Line;
if Is_A033919 (Powers_Of_Two, I) then
Max_Sequence_Number := Max_Sequence_Number + 1;
Ada.Text_IO.Put ("*****An answer was found! ");
Ada.Integer_Text_IO.Put (I, 5);
-- Ada.Text_IO.Put (" ");
Ada.Text_IO.New_Line;
end if;
exit when Sequence_Number >= Max_Sequence_Number;
I := I + 2;
end loop;
end Smallest_Number_K;
Thank you!
R. B. E. (Retired Build Engineer)